Welcome, dear reader, to this year's first MaRDI newsletter. We start off with a look at contributor roles. Or for the working mathematician: who does what (how, where, and when) in a collaborative project?
Our style of doing mathematics—while remaining largely unchanged, verifying statements using logic—has in the past fifty years acquired a variety of possible new inputs and tools. Compare our past newsletters and especially the past key article on mathematical research data to see just a few. Mathematicians nowadays attend conferences and discuss with colleagues, just like they did in the past, and they also meet online, use shared documents on platforms for LaTeX editing or git, consult online databases like the Small Groups library or online encyclopedia of integer sequences. They programsmall scripts to solve problems or find counterexamples, ask the computer to do calculations they know are cumbersome but simple by hand, write project reports and funding proposals, and much more! Our main article will shed light on how doing mathematics has changed over the past decades, showcasing tools supporting our work these days and untangling roles in collaborative and interdisciplinary projects. For a sneak preview, have a look at the illustration below. Whom can you spot doing what?
by Ariel Cotton, licensed under CC BY-SA 4.0.
Which roles did you have when writing a research paper? In our survey, you can mark all roles you ever had. For more information about these roles see the Contributor Roles Taxonomy.
We plan to report on the results in a future newsletter.
Also in this current issue of the newsletter, we additionally report from math software workshops, the love data week, and our friends around the NFDI.


A Modern Toolbox for Mathematics Researchers
What mathematicians need
It is often said that mathematicians only need pen and paper to do their job. Some elaborate on it as a joke by saying that a trash bin is also necessary, unlike the case of philosophers. Other quotes involve the need for coffee as fuel to feed the theorem-producing devices that are mathematicians. Jokes aside, it is true that mathematics research requires, in general, a relatively small infrastructure and instruments compared to other, more experimental research fields. However, two conditions are universally needed for research. Firstly, researchers need access to prior knowledge. This is addressed by creating publications and specialized literature and collecting resources in libraries and repositories to offer access to that knowledge. Secondly, researchers need to interact with other researchers. This is why researchers gather in university departments and meet at conferences. Many mathematicians love chalk and blackboard. While this is another method of writing, it serves an exchange purpose, it allows two or more people, or a small audience, to think simultaneously on the same topic.
These needs (literature and exchange spaces) are universal, have been unchanged for centuries, and will remain the same for the future. The basic toolset (pen and paper, books and articles, university departments, conferences, chalk and blackboard…) will likely stay for a long time. However, the work and practice of science researchers in general, and mathematics researchers in particular, evolves with the times of society and technology. Today’s researchers require some other specialized tools to address specific needs in contemporary research. They use digital means to have practical access to the literature, and to communicate quickly and efficiently with colleagues; they use the computing power of machines to explore new fields of math; they use managing tools to handle big amounts of data, and to coordinate distributed teams to work together. In this article, we will walk through some of the practical tools that changed the practice of mathematics research at some point in history. Some of these tools are technological changes that impacted all of society, such as the arrival of the web and the information era. Some are a consequence of changes in the way the mathematics field evolves, such as the increasingly data-driven research in mathematics that MaRDI aims to help support. We will also review some initiatives that try to change some current common practices (the CRediT system for attributing authorship), and finally, we will speculate with some tools that may one day become a daily resource for mathematicians (the impact of formalized mathematics in the mathematical practice)
From the big savants to an army of experts
We could start revisiting history with the Academy of Athens or the Library of Alexandria as “tools and infrastructure” for mathematicians in ancient times. Instead, we will directly jump to the 17th and 18th centuries, with some giant figures of mathematics history like Descartes, Newton, Leibniz, or Gauß. They were multidisciplinary scientists making breakthroughs in mathematics, physics, applied sciences, engineering, and even beyond, like philosophy. Mathematics at the time was a cross-pollinating endeavor, in which physics or engineering problems motivated mathematics to advance, and math moved the understanding of applied fields forward. The community of these big savants of the time was relatively small, and they mostly knew about each other. They mainly used Latin as a professional communication language, since it was the cultivated language learned in every country. They maintained correspondence by letter between them and published their works generally as carefully curated volumes since publication and distribution was a costly process. Interestingly, it was also in the 17th century when the first scientific journals appeared, the Philosophical Transactions of the Royal Society and the Journal des Sçavans of the French Academy of Sciences (both started around 1665). These were naturally not devoted only to mathematics or to a specific science, but more to a very inclusive notion of science and culture. Still, the article format quickly became the primary tool for scientific communication.
Fast-forward a century, and in the 19 hundreds the practice of scientists changed significantly. Mathematics consolidated as a separate branch, where most mathematicians only researched mathematics. Applications still inspired mathematics, and mathematics still helped solving application problems, but by this century most scientists focused in contributing to one aspect or another. This was a process of specialization, in which the “savants” capable of contributing to many fields were substituted by experts with more profound knowledge in a concrete, narrower field. In this century we start finding exclusively mathematical journals, like the Journal für die reine und angewandte Mathematik (Crelle’s Journal, 1826). By the end of the century (and beginning of the 20th century) this specialization process that branched science into mathematics, physics, chemistry, engineering, etc. also reached each science in particular, branching mathematics into different fields such as geometry, analysis, algebra, applied math, etc. Figures like Poincaré and Hilbert are classically credited as some of the last polymathematicians, capable of contributing significantly to many, almost all the fields of mathematics.
During the 20th century, the multiplication of universities and researchers due to broader and universal access to higher education brought much more specialized research communities. The number of scientific journals proliferated accordingly, and the publication rate and the creation of articles outpaced the classical book format. With so many articles, came the need for new bibliographic tools like catalogs (Zentralblatt MATH and Mathematical Reviews date back to 1931 and 1940, respectively) and other bibliometric tools (impact factors started to be calculated in 1975). These reviewing catalogs have been, for decades, for many mathematicians, a primary means of disseminating and discovering what was new in the research community. Their (now coordinated) Mathematical Subject Classification also brought a much-needed taxonomy to the growing family tree of mathematics branches. The conference format, in some cases with many international participants, also consolidated as a scientific format, a way to disseminate results, and a measure of the prestige of institutions.
The computing revolution
The next period we will consider starts with the irruption of computers, later accelerated with the addition of the Internet and the web. Computers have impacted the practice of mathematics at two levels. On the one hand, computers seen purely as computing machines have opened a new research field in itself, computer science. Many mathematicians, physicists, engineers… turned their attention to computer science in their early days. In particular, mathematicians started exploring algorithms, and branches of mathematics not reachable before computing power was available. For instance, numerical algorithms, chaos and dynamical systems, computer algebra, statistical analysis, etc. These new fields of mathematics have developed specific computer tools in the form of programming languages (Julia, R, …), libraries, computer algebra systems (OSCAR, Sage, Singular, Maple, Mathematica…), and many other frameworks that are now established as essential tools for the daily practice of these mathematicians.
On the other hand, computers have impacted mathematics as they have impacted every other information-handling job: as office automation. Computers help us to manage documents, create and edit texts, share documents, etc. One of the earliest computer tools that most profoundly impacted mathematicians' lives has been the TeX typesetting system. Famously, TeX was created by computer scientist Donald Knuth in more than a decade (1978 - 1989) to typeset his Art of computer programming. However, many use the more popular version LaTeX (or “TeX with macros, ready to use”) released by Leslie Lamport in 1984. Before TeX/LaTeX, including formulas in a text was done either by treating them as images (that someone had to draw manually into the final document, or engrave them into printing plates), or by semi-manual processes of composing formulas by templates on the physical font types. This was a tedious process that was only carried out for printing finished documents, not for drafts or early versions to share with colleagues. With TeX, mathematicians (and physicists, engineers…) could finally describe formulas as they intended to be displayed, and be processed seamlessly with the rest of the text. This had an impact on the speed and accuracy of the publication (printing) process, but also on a new front that just arrived in time: online sharing.
The early history of internet includes first protocols for communicating computers and first military networks of computers (Arpanet), but the real booster for civil research and for society in general was the invention of the World Wide Web by Tim Berners Lee in 1989 at the CERN. It was created as a pure researchers’ tool for exchanging scientific information, and with the goal of becoming a “universal linked information system”. Almost simultaneous to the creation of the WWW was the emergence of another critical tool for today’s mathematicians: the arXiv repository of papers and preprints. Originally available as FTP service (1991) and soon after on the WWW (1993), this repository managed by Cornell University has become a reference and a primary source for posting new works in mathematics and many other research fields. Many researchers offer their preliminary articles there as soon as they are ready to be shared, before sending them to traditional journals for peer-review and publication. ArXiv thus serves a double purpose: it is a repository to host and share results (and prove precedence if necessary), and it is also a discovery tool for many researchers. ArXiv has a mailing list / RSS feed on which you can get daily news about what has been published (or is going to be published) in the specific field of your interest. ArXiv has largely replaced this discovery function previously offered by reviewing services (zbMATH, MR). These catalogs do not host the works; instead, they index and review peer-reviewed articles (zbMATH Open also indexes some categories of arXiv). As indexing tools, these services remain authoritative (complete, with curated reviews, and well maintained), and offer valuable bibliographical data and linked information, but their role as a discovery tool is no longer an undisputed feature.
The data revolution
At this point, we have probably covered the main tools of mathematicians up to the end of the 20th century, and we enter contemporary times. One of the challenges that 21st-century research is facing is data management. Most sciences have always been based on experimentation and data collection, but the scale of data collection has grown to unprecedented levels, often called “big data”. With this term, here we refer both to particular massive datasets bound to a specific project and also to the amount of projects and data (big and small) that flood the landscape of science.
Many data repositories have become essential tools for handling data types other than research papers. In the case of software, Git (2005) and Git repositories (GitHub, 2008) have emerged as the most popular source code management tools, and have mitigated or solved many problems with managing source code versions and the collaborative creation of software.
Digital Object Identifiers (DOIs, 2000) have become a standard for creating reliable, unique, persistent identifiers for files and digital objects on the ever-changing internet. Publishers assign these DOIs to the digital versions of publications, but actually, DOIs are essentially universal labels for any digital asset. Repositories such as Zenodo (2013) offer DOIs and hosting for general-purpose data and digital objects.
In the case of mathematics, as has happened with other sciences, it has dramatically increased its reliance on data, be it experimental (statistics, machine learning…), extensive collections and classifications (groups, varieties, combinatorial…), source code for scientific computing, workflow documentation on interdisciplinary fields, etc. The scientific community, and the mathematics community in particular, has grown bigger than ever, and it is challenging not only to keep track of all the advances, but to keep track of all the methods and replicate all the results by yourself. In response to that, sciences are in the process of building research data infrastructures that help researchers in their daily lives. Here is where MaRDI (and the NFDI for other branches of science) enters as a project to help on that front.
Structuring research data implies, on one hand, creating the necessary infrastructure (databases, search engines, repositories) and guiding principles that govern ethically and philosophically the advancement of science. The FAIR principles (research data should be Findable, Accessible, Interoperable, and Reusable) that we have discussed extensively in previous articles provide a practical implementation of such principles, together with common grounds such as verifiability of results, neutrality of the researcher, or the process of the scientific method. On the other hand, the structuring of research data won’t be successful unless the researchers embrace new practices that are not perceived as imposed duties but are reliable, streamlined tools that make their results better and their work easier.
MaRDI aims to become a daily tool to help mathematicians and other researchers in their jobs. Some of the services that MaRDI will provide include accessing numerical algorithms, richly described, benchmarked, and curated for interoperability; browsing object collections and providing standardized work environments for algebraic computations (software stacks for reproducibility); curating and annotating tools and databases for Machine Learning and Statistical analysis; describing formal workflows in multi-disciplinary research team; and more. All MaRDI services will be integrated into a MaRDI portal that will serve as a search engine (for literature, algorithms, people, formulas, databases, services, et cetera). We covered some of MaRDI services in previous articles and will cover more in the future.
The cooperation challenge
Another challenge many sciences face, and increasingly in mathematics, is the growth of research teams for a concrete research project. In many experimental or modeling fields it is not uncommon to find long lists of 8, 10, or more authors signing an article, since it is the visible output of a research project involving that many people. Different people take different roles: from the person who devised the project, the one who carried out experiments in the lab, the one who analyzed the data, the one who wrote some code or ran some simulations, the one who wrote the text of the paper, etc. Listing all of them as “authors” does not give hints about their roles, and ordering the names by relative importance is a very loose method that does not improve the situation much. This challenge requires a new consensus of good scientific practice that the community accepts and adopts. The most developed proposed solution is the CRediT system (Contributor Roles Taxonomy), a standard classification of 14 roles that intends to cover all possible ways that a researcher can contribute to a research project. The system is proposed by the National Information Standards Organization (NISO), a United States non-profit standards organization for publishing, bibliographic, and library applications.
For reference, we list here the 14 roles and their descriptions:
- Conceptualization: Ideas; formulation or evolution of overarching research goals and aims.
- Data curation: Management activities to annotate (produce metadata), scrub data and maintain research data (including software code, where it is necessary for interpreting the data itself) for initial use and later re-use.
- Formal Analysis: Application of statistical, mathematical, computational, or other formal techniques to analyze or synthesize study data.
- Funding acquisition: Acquisition of the financial support for the project leading to this publication.
- Investigation: Conducting a research and investigation process, specifically performing the experiments, or data/evidence collection.
- Methodology: Development or design of methodology; creation of models.
- Project administration: Management and coordination responsibility for the research activity planning and execution.
- Resources: Provision of study materials, reagents, materials, patients, laboratory samples, animals, instrumentation, computing resources, or other analysis tools.
- Software: Programming, software development; designing computer programs; implementation of the computer code and supporting algorithms; testing of existing code components.
- Supervision: Oversight and leadership responsibility for the research activity planning and execution, including mentorship external to the core team.
- Validation: Verification, whether as a part of the activity or separate, of the overall replication/reproducibility of results/experiments and other research outputs.
- Visualization: Preparation, creation and/or presentation of the published work, specifically visualization/data presentation.
- Writing – original draft: original draft – Preparation, creation and/or presentation of the published work, specifically writing the initial draft (including substantive translation).
- Writing – review & editing: Preparation, creation and/or presentation of the published work by those from the original research group, specifically critical review, commentary or revision – including pre- or post-publication stages.
The recommendation for academics is to start applying these roles to each team member in the research projects, keeping in mind that one or more people can fulfill one or more than one role, and only applicable roles should be used. A degree of contribution is optional (e. g. ‘lead’, ‘equal’, or ‘supporting’).
Using author contributions can be pretty straightforward. For example, imagine a team of four people working on a computer algebra project. Alice Arugula is a professor who had the idea for the project, discussed it with Bob Bean, a postdoc, and both developed the main ideas. Then Bob involved Charlie Cheeseman and Diana Dough, two PhD students who programmed the code, and all three investigated the problem and filled in the results. Bob and Diana wrote the paper, Charlie packed the code into a library and published it in a popular repository, and Alice reviewed everything. They published the paper, and all of them appeared as authors. Following CRediT and publisher guidelines, they included a paragraph at the end of the introduction that reads:
Author contributions
Conceptualization: Alice Arugula, Bob Bean; Formal analysis and investigation: Bob Bean (lead), Charlie Cheeseman, Diana Dough; Software: Charlie Cheeseman, Diana Dough; Data curation: Charlie Cheeseman; Writing - original draft: Bob Bean, Diana Dough; Supervision: Alice Arugula.
For publishers, the CRediT recommendation is to ask the authors to detail their contribution, list all the authors with their roles”, and ensure that all the contributing team assume their share of the responsibility assigned by their role. Technically, publishers are also asked to make the role description machine-readable using the existing XML tag descriptors.
Formalized mathematics
We’ll finish with a more speculative tool that mathematicians may use in their mid-term future. A branch of meta-mathematics that is already mature enough to spread across all other mathematics areas is formalized mathematics. Once just studied theoretically as part of formal logic or as the fundamentals of mathematics, now computers and formal languages can transcribe mathematical definitions, statements, and proofs in a machine-readable and machine-processable way so that a computer can verify a proof. Computer-assisted proofs are now generally accepted in the mainstream (at least concerning symbolic computations), a long time passed from the “shock” of the four-color theorem and other early examples in the 70s and 80s of the necessary role of computing in mathematics. Beyond using a computer for a specific calculation that helps in the course of a proof, formalized mathematics brings the possibility of verifying the whole chain of arguments and logical steps that prove the statement of a theorem from its hypothesis. The system and language Coq was used by Georges Gonthier to formalize the aforementioned four-color theorem in 2005 and the Feit-Thompson conjecture in 2012. More recently, the LEAN system has shown to be helpful in backing up mathematical proofs such as the condensed mathematics project by Peter Scholze in 2021, or the polynomial Freiman-Ruzsa conjecture by Tim Gowers, Terence Tao, and others in 2023.
Proponents of the “formalized mathematics revolution” dream of a future in which all research articles will be accompanied by a machine-readable counterpart that encodes the same statements and proofs as the human-readable part. At some point, AI systems could help translate human-to-machine. Then verification and peer-reviewing the validity of a result will become a trivial run of the code in a system, leaving human intervention to purely language clarity and style of speech matters. Some even speculate that when logical deduction techniques can be made machine-encoded, artificial intelligence systems can be trained to optimize, suggest, or generate new results in collaboration with human mathematicians.
Whether those formalized languages remain a niche tool or become a widespread practice for mathematicians at large, and whether mathematical research will one day be assisted by artificial systems, are open questions to be seen in the next few decades.

The video is available under the CC BY 4.0 license. You are free to share and adapt it, when mentioning the author (MaRDI).
In Conversation with Bettina Eick
In this issue of the data date series, decade-long developer of the small groups library in GAP, Bettica Eick, tells us about how research has changed for her with the increasing availability of technical infrastructure.
Data ❤️ Quest
MaRDI developed the fun interactive online adventure Data ❤️ Quest. In this short game, you will find your character at a math conference, where you can interact with different mathematicians. Find out about their kind of mathematical research data and complete their quests. Prompts will guide you through the storyline, the game ends automatically after 5 minutes. Of course, you can play as many times as you like. Visit our MaRDI page with more instructions and link to play.
The five-minute game was initially published for Love Data Week 2024. It is open source and serves as a trial for an expanded multi-player game currently in development.

15th polymake conference
This report is about the 15th polymake Conference, held on February 2nd, 2024, at the Technical University Berlin. It was embedded into the polymake developer meeting, making it a three-day event held by the polymake community.
Polymake is an open source software for research in polyhedral geometry. It deals with polytopes, polyhedra and fans as well as simplicial complexes, matroids, graphs, tropical hypersurfaces, and other objects.
The conference started with a talk by Prof. Volker Kaibel on 'Programming and Diameters of Polytopes'. His illustrative presentation set the tone for a day of engaging sessions and workshops. Attendees were able to select from a range of interactive workshops and tutorials, each allowing participants to follow along. In addition to a Polymake Basics tutorial, topics as serialization, regular subdivision, Johnson solids and quantum groups were covered.
Coming from Leipzig, our motivation for attending was driven by our MARDI-project on phylogenetic trees. Specifically, we aim to improve the ‘FAIR’ness of a website with small phylogenetic trees. Polymake developer Andrei Comăneci played a key role in implementing phylogenetic trees as data types in polymake, and worked with our MaRDI fellow Antony Della Vecchia to make them available in OSCAR, which we use for our computations. They presented their work during the "use case" session on phylogenetic trees and we learned how to make use of their software.
Despite our limited experience with polymake, we felt very welcome in the community and the collaborative spirit of experimentation and creation added a layer of enjoyment to the event. The conference provided a good balance between dedicated time for hands-on exploration and the option to seek guidance in discussions with the developing team.

6th NFDI symposium of the Leibniz Association
There is no doubt that the Leibniz Association (WGL) and its member institutions are very active within the NFDI, judging from the (now) 6th NFDI symposium of the WGL that took place on December 12th, 2023 in Berlin. In fact, it was during a coffee break in the first edition of this symposium, in 2018, where the idea of a NFDI mathematical consortium, MaRDI, was born. Five years on, 26 NFDI consortia across disciplines, including MaRDI, and Base4NFDI are working towards the goals of NFDI in building a FAIR infrastructure for research data. The first-round consortia have submitted their interim reports and are preparing their extension proposals for a possible second funding phase. So, the urgent question and main topic of the 2023 symposium was: How do we move forward? Discussion rounds covered the development of the NFDI and its consortia beyond 2025 as well as the connection to European and international research data initiatives. In particular, participants discussed the question of building "one NFDI" with the bottom-up approach, via disciplines, that have been followed so far. MaRDI was represented by Karsten Tabelow in the corresponding panel discussion. It is certain, that these questions will be the focus for the time to come. What the symposium already made obvious is that everybody is working towards the same goal and is constantly bringing in ideas for reaching it. Last but not least, Sabine Brünger-Weiland from FIZ Karlsruhe had her last official appearance as the official representative in the symposium before retirement. MaRDI owes her the conversation during the coffee break five years ago.


AI Video Series
NFDI4DS produced the video series "Conversations on AI Ethics". Each of the ten episodes features a specific aspect of AI, interviewing well-known experts in the field. All episodes are available on YouTube and the TIB AV Portal.
More information:
BERD Research Symposium
The event is scheduled for June 2024 and encompasses conference-style sessions and a young researchers' colloquium, fostering collaboration and exchange of information in research in business, economics, and social science. The event's primary focus is the collection, pre-processing, and analysis of unstructured data such as image, text, or video data. Registration deadline:
May 1st, 2024.
More information:
- in English

Call for Proposals
You may apply for funding to process and secure research data to continuously expand the offerings of data and services provided by Text+ and make them available to the research community in the long term. Multiple projects between EUR 35,000 and EUR 65,000 can be funded. Additionally, an overhead of 22% is granted on the project sum. The project duration is tied to the calendar year 2025; thus, it is a maximum of 12 months. Application deadline: March 31, 2024
More information:


In this short video "Treffen sich 27 Akronyme, oder: WTF ist NFDI?" Sandra Zänkert explains the idea behind NFDI, its current state and some challenges on the road to FAIR science.
The paper "Computational reproducibility of Jupyter notebooks from biomedical publications" by Sheeba Samuel and Daniel Mietchen examines large-scale reproducibility of Jupyter notebooks associated with published papers. The corpus here is from biomedicine, but much of the methodology also applies to other domains.
The Freakonomics Radio is a popular English language Podcast that recently published an interesting two-part series on academic fraud.
The paper "The Field-Specificity of Open Data Practices", by Theresa Velden, Anastasiia Tcypina provides quantitative evidence of differences in data practices and the public sharing of research data at a granularity of field-specificity rarely reported in open data surveys.
When your open-source project starts getting contributors, it can feel great! But as a project grows, contributors can neglect to document everything. In this situation, the article "Building a community of open-source documentation contributors" by Jared Bhatti and Zachary Sarah Corleissen may help you.
Welcome to the summer MaRDI Newsletter 2024! On the longest day of the year, we discuss “I have no data”—a statement many mathematicians would subscribe to. Our key article answers the most frequent questions and draws a brighter future for everyone—where, for instance, we believe you can search and find theorems rather than articles. Is this data? We believe it is.
by Ariel Cotton, licensed under CC BY-SA 4.0.
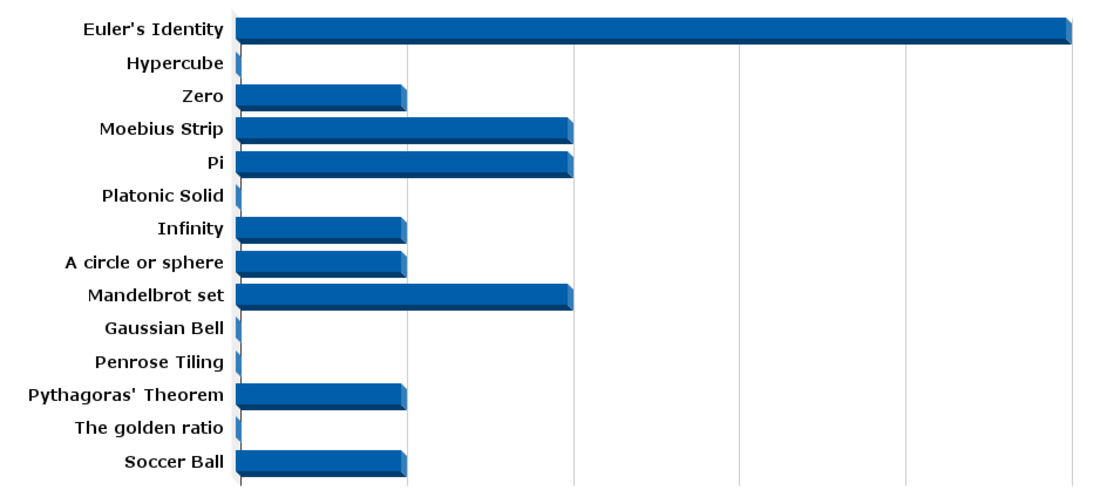
If you could select just one "item" (such as an equation, a geometrical object, etc.) to symbolize the entirety of mathematics, what would you choose?
Choose your representative here!
Also, check out our Data Date Interview with Martin Grötschel, workshop reports, and the first exhibition of the MaRDI Station on the ship MS Wissenschaft.


“I’m a mathematician and I use no data. Change my mind.”
At the MaRDI team, we continuously communicate the project's goals and mission to a general audience of mathematicians. We describe the importance of data in modern mathematics and the FAIR principles and show examples of the services that MaRDI will provide to some key communities represented in MaRDI’s Task Areas: computational algebra, numerical analysis, statistics, and interdisciplinary mathematics.
However, our audience often consists of mathematicians working in other areas of mathematics, maybe topology, number theory, harmonic analysis, or logic… who consider themselves not very heavy data users. In fact, the sentence “I have no data” is a statement that many mathematicians would subscribe to.
In this article, we transcribe fictional (but realistic) questions and answers between a “no-data” mathematician and a “research data apostle”.
I do mathematics in the “traditional” way. I read articles and books, discuss with collaborators, think about a problem, and eventually, write and publish papers. I use no data!
Maybe we need clarification on the terms. We call “Research Data” to any information collected, observed, generated, or created to validate original research findings.
If you think of a large database of experimental records collected for statistical analysis, or if you think of the source code of a program, yes, these can be examples of research data. However, there are many other types of research data.
You probably use LaTeX to write your articles and BibTeX to manage your lists of bibliography references. You probably use zbMATH or MathSciNet to find a bibliography and arXiv to discover new papers or to publish your preprints. Your LaTeX source files and your bibliography lists are examples of research data. Without a data management mindset, you wouldn’t have services like zbMATH or arXiv.
But there is more data than electronic manuscripts in your research. If you find a classification of some mathematical objects, that list is research data. If you make a visualization of such objects, that is research data. Every theorem you state and prove can be considered an independent piece of abstract research data. If you have your own workflow to collect, process, analyze, and report some scientific data, that workflow is in itself a valid piece of research data.
Many mathematical objects (functions, polytopes, groups) have properties that you can address in your theorems. For instance “since the integral of this function can be bounded by a constant C<1…”. Such properties are collected in data repositories (DLMF, etc.) that provide consistent and unified references to gather these data.
You should think of research data as any piece of information that can be tagged, processed, and built upon to create knowledge in a research field. This perspective is useful for building and using new technologies and infrastructure that every mathematician can benefit from.
I think you say “everything is data” to give the impression that MaRDI and other Research Data projects are very important… but how does your “data definition” affect me?
It is not a mere definition for the sake of discussion. We believe there is a new research data culture in which mathematicians from all fields should participate. A research data culture is a way to think about how we organize and structure all the human knowledge about mathematics, how we store and retrieve that knowledge, the technical infrastructure we need for that, and ultimately, how we make research easier and more efficient.
Imagine you are looking for some information that you need in your research. When you look for a result, the “unit of data” would be a theorem (probably together with its proof, a bibliographic reference, an authorship…), but not an article or a book on themselves. So, it is more useful to consider that your data is made up of theorems instead of articles.
Then, your theorems will fit into a greater theory in your field. Sure, you can explain this in your article and link to references in your bibliography, but you will probably not link to specific theorems, likely sometimes you will miss some relevant references, and certainly you can’t link to future works retroactively. By thinking about your results as data and allowing knowledge infrastructures to index and process them, your results will be put in a better context for others to find, access, and reuse them. Your results will reference others, and others will reference yours. Furthermore, they will withstand better the evolution and advances in the field.
I thought MaRDI was about building infrastructure to manage big databases and code projects. Since I don’t use databases or program, why should I be interested in MaRDI?
MaRDI is much more than that. It is true that mathematicians working with these types of data (large databases, large source code projects, etc. …) need a reliable infrastructure to host and share data, standards to make data interoperable, and a way to work collaboratively in large projects. MaRDI addresses these needs by setting task groups that develop the necessary infrastructure in each domain (for instance, in computer algebra or statistics).
But as we mentioned above, there are many other types of data: classifications of mathematical objects, literature (books and articles), visualizations, documentation of workflows, etc. MaRDI takes an integral approach to research data and addresses the needs of the mathematical community as a whole.
For instance, MaRDI bases its philosophical grounds on the FAIR principles. The acronym FAIR means that research data should be Findable, Accessible, Interoperable, and Reusable (read our articles on each of these principles applied to mathematical research). These principles are now widely accepted as the gold standard for research data across all scientific disciplines, and they are the grounds for all other NFDI consortia in Germany and other international research data programs.
Following FAIR principles is relevant for all researchers. Your results (your data) should be findable for other researchers, which implies caring about digital identifiers and indexing services. Delegating and thrusting third-party search engines is not a wise strategy. Your research should be accessible, meaning you should be concerned about publication models, the completeness of your data, or your meta-data structure. Your data should be interoperable, meaning you should follow common practices in your community to exchange data. At the very least, this could mean following common notation and conventions for your results so they can be translated across the literature with minimal context adaptations. Finally, you should always keep in mind that the most important FAIR principle is reusability. Reusability is the base of verifiability. Document your thought processes. Sharing insights is as important as sharing facts. Research that is not reused is barren.
MaRDI aims to spread this research data culture by raising awareness of these principles and encouraging discussions to devise best practices or address challenges in concrete, practical cases. Since these discussions affect all mathematicians, it is a good reason to be interested in MaRDI.
Furthermore, MaRDI strives to develop services that best help mathematicians. Aside from the specific services developed for the aforementioned task areas, MaRDI addresses all mathematicians with its main and central MaRDI Portal, a knowledge base to better manage all mathematical knowledge from a research data perspective. MaRDI also lays bridges to communities that can impact mathematics and the research data paradigm, like the formalized mathematics community, which is taking an increasing role in mathematical fields other than logic or theoretical computer science.
Why do you talk about political / philosophical / ethical questions? Shouldn’t MaRDI be just a technical project?
To build an infrastructure for the future of mathematical research data, planning must be accompanied by a serious reflection on the guiding principles. The FAIR principles we mentioned before are not a technical specification of concrete implementations but a set of philosophical rules that researchers should apply to their research data. The implementation and the guiding principles cannot be independent.
MaRDI encourages a debate and calls researchers to decide on challenging situations concerning research data. For instance, which are the best publication practices? Should researchers publish in traditional journals? In Open Access journals? Should they also publish a version (identical or preliminary to the final one) on preprint services such as arXiv? Should the pay-per-publish practice be accepted? How can we ensure the publication quality in that case? These questions are one particular topic related to handling research data; thus, they fall into the area of interest of MaRDI.
MaRDI will not dictate absolute answers to these questions, but it will try to stimulate and facilitate discussion about these delicate topics in the community. It will promote principles and common grounds that the entire community of mathematicians can agree on. Then, MaRDI will help build the necessary infrastructure to put these principles into practice.
MaRDI is neither a regulating agency nor a company offering products and solutions. MaRDI is a community of mathematicians. To be more precise, MaRDI is a set of different communities (computer algebra, numerical analysis, statistics and machine learning, interdisciplinary mathematics) of mathematicians that collaborate to create a common infrastructure and to promote culture for mathematical research data. MaRDI is scoped in Germany but it has a clear universal vocation, other communities of mathematicians from anywhere may complement MaRDI in the future. Thus, MaRDI is a technical project when its members, researchers who face a specific challenge, define technical specifications for the infrastructure to build. But MaRDI is at all times a social and philosophical project since its members endeavor to build the tools for mathematical research in the future.
So, should I rewrite my papers thinking on “Data”?
Research articles and books are and will probably always be the primary means of communicating results between researchers. You should write your papers thinking of your peer mathematicians who will read them. Your research paper is the first place where some theorem is proved. It gives you authorship credit, and as such, it establishes a new frontier of mathematical knowledge. But at the same time, your papers can contain several types of data that can be extracted, processed automatically, and potentially included in other knowledge bases.
Imagine your paper proves a classification result about all manifolds of dimension 6 that satisfy your favorite set of properties. What about other dimensions? What about slightly different properties? Your result fits in a broader picture to which many mathematicians contribute. At some point, it will make sense to collect all these results somewhere to have a more complete presentation. This can be a survey article/book, but sometimes it is better to have it in the form of a catalog. In this case, it would be a list of all manifolds classified by their invariants or by some characteristics. This catalog would serve as a general index, the place to look up what is known about your favorite manifolds, and from this catalog, you can get the references to the original articles.
We can go further and ask whether a catalog is the best information structure we can aim for. At MaRDI, we support knowledge graphs as a way to represent all mathematical knowledge. In a knowledge graph, every node is a piece of information (a manifold, a list of manifolds, an author, an article, an algorithm, a database, a theorem…), and every edge is a knowledge relationship (this list contains this manifold, this manifold is studied in this article, this article is written by this author…)
You can help build this knowledge graph of all mathematics by thinking about and preparing your research data for inclusion in it.
I tried the MaRDI Portal to search for one of my research topics. It returned several article references that look very much like zbMATH Open. Why do we need another search engine?
First, keep in mind that the Portal is still under development. Second, it’s not a surprise that you obtained article references looking like zbMATH Open. It is exactly where they come from. MaRDI does not intend to substitute zbMATH or any other catalog or database, instead, it aims to integrate them in a single place, with a richer structure.
zbMATH is a catalog, the MaRDI portal is a knowledge graph. The MaRDI knowledge graph includes already (partially) the zbMATH catalog, the swMATH software catalog, the Digital Library of Mathematical Functions (DLMF), the Comprehensive R Archive Network (CRAN), and the polyDB database for discrete geometric objects. Eventually, it will also include other sources like arXiv and more. The MaRDI knowledge graph imports the entries of these sources and gives them a structure in the knowledge graph. Some links on the graph are already provided by the sources, like one article reference points to other articles cited in the bibliography. A challenge for the MaRDI KG is to populate many more links between different parts of the graph, like “This R library uses an algorithm described in this article”.
Imagine this future: You learn about a new topic by reading a survey, attending a conference, or following a reference; and you think it could be useful for your research. With a few queries, you find everything published in that research direction. You can also find which researchers and universities or research institutes have people working in that field, in case you want to get in contact. You have easy and instant access to all these publications. You query for some general information that is scattered across many publications (e.g., what is known about my favorite manifolds in any dimension). You get answers that span all the relevant literature. Refining your query, you get more accurate results pointing to specific theorems which are relevant to you. Results found by automatic computation (theorems but also examples, lists, visualizations…) come with the code you can run and verify easily in a computer virtual machine. Mathematical algorithms that can be used as a pure tool to solve a concrete problem can be found and are plug-and-play into any software project. Databases and lists of mathematical objects are linked to publications, and all results are verifiable (maybe even with a formalized mathematics appendix). The knowledge graph gives you an accurate snapshot of the current landscape of mathematical knowledge, and rich connections arise from different fields. You can rely on the knowledge graph not only as a support tool to fetch references but also as your main tool to learn and contribute to mathematical research. This future is not yet here, but it is a driving force for those who build MaRDI.

The video is available under the CC BY 4.0 license. You are free to share and adapt it, when mentioning the author (MaRDI).
In Conversation with Martin Grötschel
Reflecting on his extensive career in applying mathematics, Martin Grötschel provides both a retrospective on how mathematics has shifted towards a more data-driven approach and a prospective on what the future of the field might hold.
MaRDI on board the German Science Boat
On May 14, 2024, the ship MS Wissenschaft embarked on its annual tour. During the summer months, the floating science center usually visits more than 30 cities in Germany and Austria. The theme of the exhibition is based on the respective science year in Germany. The theme of this year’s tour is freedom. Adolescents, families, and especially children are invited to visit the interactive exhibition. Admission is free of charge.
MaRDI showcases the cooperative multi-player game “Citizen Quest: Together for a freer world”. Players navigate a city environment, where citizens are confronted with dilemmas and issues related to mathematical research data and various other facets of freedom. The adventure begins aboard a mathematical vessel recently docked in the city’s harbor. Here, advocates of scientific freedom promote the sharing of research data in a FAIR (findable, accessible, interoperable, reusable) manner. The users meet different characters and help them with different quests - for example help a young programmer who wants to make his newly developed computer game about his dog accessible to his friends, debunk a fake news story, learn about ethical aspects of AI surveillance, and help researchers who developed a tool to identify dinosaur footprints get reusable test data... Many small quests need to be solved!
Workshop "Bring Your Own (Mathematical) Model"
On Thursday, 02.05.2024, MaRDI team members hosted the "Introduction to the preparation of mathematical models for the integration in MaRDI's MathModDB (Database of Mathematical Models)" workshop within the framework of the Software & Data Seminar series at Weierstrass-Institute for Applied Analysis and Stochastics (WIAS), Berlin. The workshop focused on templates developed recently by MaRDI's "Cooperation with other disciplines" task area, the templates facilitating the process for researchers wishing to add mathematical models to the MathModDB. The templates are written as Markdown files and designed to have a low barrier to entry allowing users with little to no experience to get started easily while guaranteeing the important details of the mathematical model are gathered. The filled-in templates would then serve as a basis for a further semantically annotated standardized description of the model employing the MathModDB ontology. These semantically enriched models can then be added to the MathModDB knowledge graph (database of mathematical models) making them findable and accessible.
The workshop consisted of two parts: a short introductory talk followed by a hands-on exercise session. The talk gave the participants an introduction to the FAIR principles and to the difficulties of making mathematical models FAIR. Next, MaRDI's approach to that problem was explained which is based on ontologies and knowledge graphs. In preparation for the hands-on exercise session, the MarkDown template was presented and the audience was shown an example of how to use it. During the exercise session, five WIAS researchers with different scientific backgrounds filled in templates with their mathematical models. The topics of the mathematical models included Maxwell equations, thin-film equations, a poro-visco-elastic system, a statistical model about mortality rates, and a least-cost path analysis in archeology. The templates filled-in by the participants will be integrated into the MathModDB knowledge graph by MaRDI experts in the near future.
In general, the workshop was successful in raising awareness about MaRDI and FAIR principles while directly engaging the participants in providing information about the mathematical models they use. There were lively discussions not only about technical details of the templates and possible further improvements, but also about more general concepts and features that would improve for example reusability of model descriptions. MaRDI's MathModDB team plans to develop the template further based on valuable input received during the workshop, and is looking forward to carrying out future field tests.

Workshop on Scientific Computing
The MaRDI "Scientific Computing" task area focuses on implementing the FAIR principles for research data and software in scientific computing. The second edition of their workshop (Oct 16 – 18, 2024, in Magdeburg) aims to unite researchers to discuss the FAIRness of their data, featuring presentations, keynote talks, and discussions on topics like knowledge graphs, research software, benchmarks, workflow descriptions, numerical experiment reproduction, and research data management.
More information:
- in English
EOSC Symposium 2024
The symposium will take place from 21 to 23 October 2024 in Berlin. It is a key networking and idea exchange event for policymakers, funders, and representatives of the EOSC ecosystem. The symposium will feature a comprehensive program, including sessions on the EOSC Tripartite Partnership, collaborations with the German National Data Infrastructure (NFDI), and a co-located invitation-only NFDI event.
More information:
- in English

From proof to library shelf
This workshop on Research Data Management for Mathematics will take place at MPI MiS in Leipzig from November 6-8, 2024. It will offer feature talks, hands-on sessions, and a Barcamp to discuss mathematical research data, present ideas and services, and network.
More information:
- in German


The review Making Mathematical Research Data FAIR: A Technology Overview by Tim Conrad, Eloi Ferrer, Daniel Mietchen, Larissa Pusch, Johannes Stegmuller, and Moritz Schubotz provides a technology review of existing data repositories/portals focusing on mathematical research data.
In the paper A FAIR File Format for Mathematical Software, Antony Della Vecchia, Michael Joswig, and Benjamin Lorenz introduce a JSON-based file format tailored for computer algebra computations, initially integrated into the OSCAR system. They explore broader applications beyond algebraic contexts, highlighting the format's adaptability across diverse computational domains.
The video FAIR data principles in NFDI by NFDI4Cat provides an in-depth exploration of research data management tools and FAIR data principles. The video also examines how these tools are applied in experimental setups. Whether you're a researcher, data enthusiast, or simply curious about the future of data management, this video will provide valuable insights and actionable takeaways.
The position paper A Vision for Data Management Plans in the NFDI by Katja Diederichs, Celia Krause, Marina Lemaire, Marco Reidelbach, and Jürgen Windeck envisions an expanded role for Data management plans within Germany's National Research Data Infrastructure (NFDI), proposing their integration into a service architecture to enhance research data management practices.

Welcome back to a new issue of the MaRDI newsletter after a hopefully prosperous and colorful summer (or winter, depending on your location on Earth). Mathematical research data is usually independent of seasons, color, or location. However, our current topic does combine geographic maps and colors – the four-color theorem.
by Ariel Kahtan, licensed under CC BY-SA 4.0.
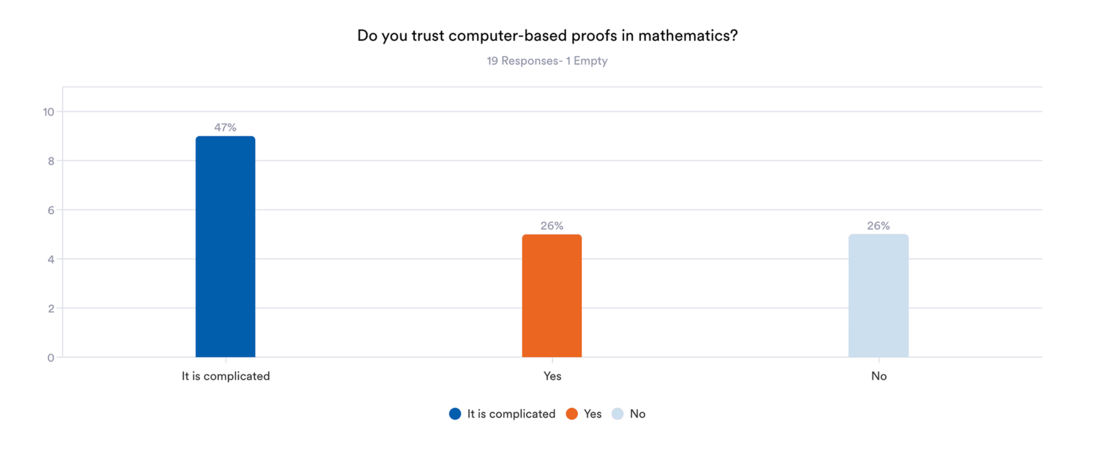
The main article of our newsletter will take you on a journey through time, technology, and philosophy, raising questions such as: What constitutes a proof? How much can we trust computers (and their programmers)? and How much social aspect is there in writing mathematical proofs? In the Data Date section, you will meet Yves Bertot, a computer scientist who is the maintainer of the official Coq four-color theorem repository on GitHub. In our one-click survey, we ask you to answer the question:
Do you trust computer-based proofs in mathematics?
In June, we asked you to select one "item" to symbolize the entirety of mathematics. Here are your results:
Some of you also suggested new items. Among these were the Hopf fibration, axioms, and a topological manifold.
by Ariel Kahtan, licensed under CC BY-SA 4.0.
A lost and found proof
The four-color theorem is a famous result in modern mathematics folklore. It states that every possible map (any division of the plane in connected regions, like a world map divided into countries, or a country divided into regions) can be colored with at most four colors in a way such that adjacent regions do not share the same color. Like many famous theorems in mathematics, it has a simple enough statement that anyone can understand and a fascinating story behind it. This was the first major theorem in pure mathematics for which its proof absolutely needed the assistance of a computer. But more interestingly for us, the story of the four-color theorem is a story of how Research Data in Mathematics became relevant and how mathematicians were led to debate questions such as “How do we integrate computers into pure mathematical research?”, or more fundamentally, “What constitutes a proof?”. The story goes like this:
A problem of too many cases
In 1852, a young Englishman by the name of Francis Guthrie was playing to color the counties of England, avoiding neighboring counties to have the same color. In the England map case, he managed to do it with four colors, and he wondered if any conceivable map would also be colorable with only four colors. The problem of coloring regions of a map is equivalent to coloring the vertices of a planar graph. To build that graph, take one vertex per region and join two vertices if the corresponding regions are adjacent (see the illustration accompanying this article). If you start with a map, you obtain a planar graph (the edges can be drawn so they do not cross each other), and every planar graph can be converted into a map. This is therefore a problem in graph theory. Francis asked his brother, Frederick, a student of mathematics, who in turn asked his professor, Augustus de Morgan. De Morgan could not solve it easily and shared it with Arthur Cayley and William R. Hamilton, and after a while, it caught some interest in the mathematical community.
It was more than 20 years later, in 1879, when Alfred Kempe, a barrister with some mathematical inclinations, published a proof with many elegant ideas [Kem79]. Kempe’s proof was accepted as valid for some years, but unfortunately, Percy Heawood found it erroneous in 1890. Kempe’s strategy, however, was right, and it was the basis for all subsequent attempts to prove the conjecture. It went like this: First, find a finite set of “configurations” (parts of a graph) such that every hypothetical counterexample must contain one of such configurations (we call it an unavoidable set of configurations). Second, for each one of these configurations, prove that if it can be colored with five colors, then we can rearrange the colors such that only four are used (we say that it is a reducible configuration). The existence of such a set of unavoidable reducible configurations proves the theorem (if there was a minimal counter-example map needing five colors, it would contain one such configuration, but then it would be possible to re-color it with only four). Kempe’s proof used a set of only four configurations, that he checked one by one. Unfortunately, he failed to see one possible sub-case when checking one of them. Kempe’s original proof could not be fixed, but many mathematicians became gradually convinced that the solution would come from having a (much) larger set of unavoidable reducible configurations. It was a problem of enumerating and checking a huge number of cases.
The problem remained open for eight more decades, with many teams of mathematicians racing for the solution in the 60s and 70s. In 1976, mathematicians Kenneth Appel and Wolfgang Haken finally made a valid proof [AH77a], [AHK77]. Their method, however, was a bit unorthodox. Haken was already a renowned topologist, and Appel was one of the few people who knew how to program the new mainframe computer that their university (University of Illinois) had recently purchased. Together, they developed a theoretical argument that reduced the proof to check 1,936 configurations that had to be analyzed independently. Then, they used the newly available computers to write a program that verified all cases, completing the proof. They published their result as a series of long articles [AH77a], [AHK77], supplements [AH77b], [AH77c], and revised monographs [AH89], filled with long tables and hand-drawn diagrams representing every case and its analysis, collected manually in a pre-databases era.
Appel and Haken's proof was controversial at the time. Many mathematicians could understand the theoretical parts of the proof, but one needed a computer scientist to program the code. Programming was quite a rare skill for mathematicians in 1976. Even if you understood both the math and the algorithm, you needed to implement it. The program was originally made in the assembly language of the IBM 370 mainframe system, which, again, was not available to everybody. And even if you had all the pieces, you would have to trust the processors of the computer, and even then, you could have the uncertainty that maybe there is some typo in the code, maybe you forgot a case to be checked, or maybe you overlooked something on the tedious visual inspections of the diagrams (actually, several minor typos were found and fixed in the original articles). Nevertheless, the mathematical community mostly celebrated the achievement. Postal stamps were issued in commemoration, and it made to the scientific and even mainstream news [AH77d].
In 1995, almost twenty years later, mathematicians Neil Robertson, Daniel Sanders, Paul Seymour, and Robin Thomas tried to replicate Appel and Haken’s proof with a more modern computer. In the process, they found it so hard to verify (understanding and implementing the algorithms) that they eventually gave up and decided to make their own proof [RSST96]. It was a substantial modification, making it more streamlined. In particular, they reduced the number of cases to be checked to 633. Still too many to be checked by hand, but an improvement anyway. They also used a higher-level programming language, C, and they made the source code available through a website and an FTP server at their university.
The last stop in our story came in 2005 by computer scientist Georges Gonthier. Originally aiming for a proof of concept that computers can help in formal logic, Gonthier managed to translate Robertson et al. proof into a fully formalized, machine-readable proof of the four-color theorem, using the system and language Coq [Gon05], [Gon08]. To verify the truthness of the theorem, one does not need to verify the 60 000+ lines of code of the formalized proof, but it is enough to verify that the axioms of the system are correct, that the statement of the theorem is correct, and that the Coq engine spits out a “correct compilation” meaning that every step in the proof code is a logical consequence of the previous ones. You still need the computer, but the things to trust (axioms, system engine, the Type Theory that provides a theoretical framework ) are not specific to the theorem at hand, and arguably thousands of researchers have checked and verified the axioms and the engine for reliability. The four-color theorem was used as a benchmark, as a test example to prove the capabilities of the Coq system. The Feit-Thompson theorem in group theory was another example of a long and tedious proof that was formalized into Coq, removing any doubt that some typo or hidden mistake could ruin the Feit-Thompson proof. But more importantly, it demonstrated that formalized mathematics was capable of describing and verifying proofs of arbitrarily complex and abstract mathematics.
The reader interested in the details of the four-color theorem’s history and the main ideas of the proof can check the references in the “Recommended readings” section of this newsletter. Instead of digging further into history, we will make a particular reading of this story focusing on how it changed our view of mathematics through the lens of Research Data.
The innovations used in the proofs of the four-color theorem prompted two major changes in the philosophical conception of mathematics and proof: first, the use of computers to assist in repetitive verification tasks, and second, the use of computers to assist in logical deductions.
The computer-assisted proofs revolution
When Appel and Haken announced their proof, they sparked many uncommon reactions in and outside the mathematical community. Instead of the cheer and joy of solving a century-old problem, many mathematicians showed unease and dissatisfaction with the fact that a computer was necessary to find and check thousands of cases.
Most of the community accepted the result as valid, but not everybody was so happy. Many believed that a shorter and easier proof could be found by cleaning Appel and Haken’s argument, and they hoped that, although computers were used to find the list of cases to check, once found the verification could be done without computers. In a despicable episode [Wil16], Appel and Haken were once rejected to speak at a university by the head of the mathematics department on the grounds that their proof was completely inappropriate and, at the same time, no professional mathematician would work anymore on the problem to find a satisfactory proof. Thus, it was argued, that they had done more harm than good to the mathematical community, and they did not deserve publicity, nor should students be exposed to these ideas.
In public, intellectuals also had their confrontations. In 1979, philosopher Thomas Tymoczko published a paper, The Four-Color Problem and Its Philosophical Significance [Tym79], in which he defended the idea that the four-color theorem was not proven in the traditional meaning of the word “prove”, and that either it should be considered unproven until a human could read and verify the proof, or the meaning of “proof” should be redefined as a much weaker sense. For Tymoczko, a proof must be convincing, surveyable, and formalizable. While all experts in the four-color theorem were eventually convinced, and the computer provided evidence that there was a formal argument proving the theorem, Tymoczko argued that the proof was not surveyable, meaning that no human could follow all the calculations and details. The mathematician Edward R. Swart replied against Tymoczko with the article The Philosophical Implications of the Four-Color Problem [Swa80], where he defended the validity of Appel and Haken’s method, envisioning a future where computing tools would be integrated into mathematicians' practice.
The philosophical debate in the 70s and 80s also highlighted some social and generational aspects of the mathematical community. Older mathematicians had high concerns that the part of the proof that depended on the computer could have some mistakes, or the computer could have had a “glitch” and made a mistake. A younger generation of mathematicians could not believe that the hundreds of pages with hand-made computations and drawings were reliable. But more importantly, it was the lack of an easy verification procedure that concerned the whole community.
Today, the use of computers is standard practice among mathematicians. Not only as a help in office tasks (exchanging emails, typesetting in LaTeX, publishing on journals or repositories…), but also as a core tool for mathematical research, including numerical algorithms, computational algebra, classification tasks, statistical databases, etc. It took many decades to be convinced that using computers does not necessarily mean doing applied mathematics or being engineering-oriented. In the process, however, we learned that using computers requires some good practices to handle the data associated with them, not the least the FAIR principles of research data, and the importance of open access for verifiability.
The lost and found proofs. A cautionary tale of Research Data.
The four-color theorem is paradigmatic of why a research data perspective is necessary in modern mathematics. This theorem put on the table for the first time philosophical and practical questions of what constitutes a proof, how much we can trust computers (and their programmers), or how much social aspect is there in writing mathematical proofs.
In some sense, the four-color theorem has been “lost” or “almost lost” several times. The first time was when Kempe’s proof was found erroneous. This highlights the importance of verifying proofs and the fact that many errors and gaps can be subtle and difficult to spot.
The second time is more difficult to associate with a precise event. When Appel and Haken’s proof was found, it was verified by them (with the help of a computer) and to some extent by a relatively small group of mathematicians in their community. That was a quite competitive community, a true race took place to be the first to provide complete proof of the four-color theorem. Every expert in the problem had the opportunity to check Appel and Haken’s proof, by comparing the published calculations with their own and having direct exchange with the two authors. All these experts agreed unanimously that the proof was valid, so the mathematical community at large was convinced of its validity, though some dissonant critics argued against that recognition. Then, some years passed, and nobody else was interested in re-checking Appel and Haken’s algorithm. When a new generation of mathematicians (Robertson et al) tried to replicate it, they found it was unfeasible. They had no code to test, the algorithm was not entirely clear, and they would have to enter manually hundreds of cases. The proof was effectively lost*.
Let us note that in the late 70s, computers were highly advanced laboratory equipment. Most mathematicians would not have access or know how to operate these devices. Operating systems were in their infancy, and most programs were only able to run in a specific hardware architecture, depending on the brand or even model (like the IBM 370 mainframe). The most reliable way of sharing a program was to describe the algorithm verbosely or with flow diagrams and leave to the receiver the task of implementing it in their machine architecture. Appel and Haken published their proof originally in two parts [AH77a], [AHK77], and then provided two supplements[AH77b], [AH77c], with more than 400 pages of calculations, as computer outputs (the output interface of the computer was not a screen, but a teletype, it printed characters on paper). Keep in mind that this was before TeX and LaTeX, so all the text was set with a typewriter, hand-written formulas, and hand-drawn diagrams. The supplements were not published directly, but instead, they were produced as microfiches, a support consisting of microphotographs on a film that could be read with an appropriate device with a magnifying lens and a light source, like a film slide. There was only a very limited number of copies of these microfiches deposited in some university libraries.
Appel and Haken faced a new situation when publishing their result. From a practical point of view, they wanted to share as much information as possible to make the proof complete (to be convincing, as surveyable as possible, and to demonstrate it was formally flawless). They just had no repositories, no internet, and no practical way to share scientific code in a way that it would be possible to reuse. In today’s terms, the part of their proof that used computers met none of the FAIR principles. Of course, this judgment would be anachronic and not fair (pun intended). It is precisely because of their pioneering work that the mathematical community started realizing that better standards were necessary.
It took Robertson et al. more than a year to develop a new proof, which was an improvement with respect to Appel and Haken’s in several aspects (fewer cases to check, streamlined arguments). This time, they had some interoperable tools (e.g., the C programming language, which would compile in any personal computer), and exchange methods suited to code (websites, FTP), so they made all the source code fully open and available. In modern terms, we would say that, with respect to Appel and Haken’s data, they improved the findability and accessibility by setting up the web and FTP, the interoperability by using the C language, and the reusability given the later reuse by Gonthier.
Today, we have better FAIR standards (indexing the data, hosting it at recognized repositories, etc.), but again, it would be anachronical to blame them. If the original web and FTP server that hosted the code had disappeared, it would have been the third time that the proof had been lost, and for the very mundane reason that nobody kept a copy. Their servers did disappear eventually, but certainly, there were copies, and today, the original files can be found for instance in arXiv, uploaded by the same authors in 2014 [RSST95]. This is a much more robust strategy for findability and accessibility and aligns with today’s standards.
Interestingly, Robertson et al. deliberately used the computer also for the part of the argument that Appel and Haken had managed to describe by hand. If one needs to use the computer anyway, then let’s use it for all tedious calculations, not only those exceeding human capabilities. In the end, the computer is less prone to make mistakes due to fatigue in a repetitive task.
Gonthier brought that idea to the extreme: What if all the proof could be set up to be checked by the computer, not only the repetitive verification of cases? What if a computer was also less error-prone in following a logical argument? When Gonthier started his work on the four-color theorem, the proof was certainly not lost (Robertson et al.’s proof was the basis for Gonthier), but it was missing some FAIR characteristics it never had. Verifiability, which is the close cousin of Reusability, was still a weak point of the theorem.
In the new millennium, when computers were personal and the internet was transforming the whole society, the old philosophical debate about what constitutes a proof, and how verifiable is a proof that is not entirely surveyable, but that it was formalizable was put again in the spotlight. However, this time, the question wasn’t if computers should have a role in mathematical proofs, but instead, the pressing issue was: what are the good standards and practices that we should have for the role that computers certainly play in mathematics and all sciences?
The formalized mathematics revolution
Security in computing is a field that most people associate with cryptography to send secret messages, identity verification to prove who you are online, or data integrity to be sure that the data is not corrupted by error or tampering. However, there is a branch of computer security that tries to guarantee that your algorithms (theoretically) always provide the intended result without edge cases or special inputs that produce unexpected outputs. A related field of research is Type Theory, which has been in development since the 60s of last century. In programming languages, a “type” is a kind of data or variable, like an integer, a floating point number, a character, or a string. Many programming languages detect type mismatch, like a function that takes an integer as its argument will throw an error if a character is passed. But usually, the type identification is not more sophisticated than basic types. If a function, say, only accepts prime numbers as input, the machine should be able to verify that the passed argument is a prime number and not just an integer. Similarly, the system should verify that a function that claims to produce prime numbers does not produce other integers as output. From this starting point, one can develop a theory and prove that verifying types is equivalent to verifying logical propositions and thus equivalent to proving abstract theorems. A function takes a hypothesis statement as input and produces a thesis statement as output, so verifying that types match when chaining functions is equivalent to checking that you can apply a lemma in a step of proving a theorem. In 1989 Coq ** was released, a software and language for proving theorems based on Type Theory. This was the system used (and developed) by Gonthier to formalize the four-color theorem.
How could one be sure that Robertson et al’s proof (or Appel and Haken’s) did not forget any case in their enumeration? Or that cases were not redundant? Or that all the logical implications produced mechanically in the case verification process were correct? Since the proof was not surveyable by hand, there would always be a cast of doubt. But with the new formalized proof, that doubt dissipates. In this new scenario, one can cast doubts about the Type Theory on which it is based (which is a mathematical theory largely made of theorems proven in the most traditional sense of the word, but some set-theoretical issues still cause itches), or on the software implementation, or on the hardware it runs into. But all these are global concerns, not specific about the four-color theorem. If we accept the Coq system as reliable, then the four-color theorem is a truthful theorem since the formal proof by Gonthier passes the compilation check in Coq.
Certainly, Gonthier was not particularly concerned about the possibility of an error that Appel and Haken or Robertson et al had missed. Instead, Gonthier’s goal was to show that any mathematical proof of a theorem, no matter how abstract, lengthy, or complex it was, would be possible to translate into a formal proof verifiable by a computer. The four-color theorem was a useful benchmark. In fact, a significant part of Gonthier’s work provided the foundation to properly define the objects in question. For instance, to be rigorous, planar graphs are not purely combinatorial objects, they concern intersections of lines in the plane, and hence require continuity and the topology of real numbers. Building all these fundamental blocks meant enormous preparation work even before looking at Robertson et al. proof. The next major proof Gonthier formalized was the Feit-Thompson theorem (any finite group of odd order is solvable), which proof takes 255 pages and was famously convoluted even for the specialists at the time it appeared in 1963. It was another benchmark theorem, which in this case required defining complex algebraic structures (groups, rings, modules, morphisms…), but it also shared some structures with the four-color theorem, so it was somehow a natural development.
Gonthier’s goal was fulfilled, formalized mathematics is considered today a mature enough branch of mathematics. Other theorem provers, such as LEAN, have appeared following the path started by Coq. Recently, some results in mathematics have been proved using such systems, making them useful for finding new results (as opposed to formalizing already known and proven theorems), including the condensed mathematics project by Peter Scholze in 2021, or the polynomial Freiman-Ruzsa conjecture by Tim Gowers, Terence Tao, and others in 2023, both using LEAN.
To avoid losing this formalized proof of the four-color theorem in Coq in the future, it is now part of the standard packages of the Coq installation, has its own GitHub repository, and has a small team of maintainers that ensures that the proof compiles successfully with new releases of the Coq engine (see the interview with Yves Bertot in this newsletter).
The four-color theorem proofs have had some direct continuation in other related works. In 2021, Doczkal [Doc21] used Coq’s formal proof and the provided infrastructure in graph theory, namely the hypermaps structures devised by Gonthier, to formalize a related result in graph theory, Wagner’s theorem for characterizing planar graphs. In a different direction, Steinberger [Ste10] made a new version of Roberson et al.’s proof in 2009, in which he trades volume for simplicity. He gives a large set of configurations, but all of them are simpler to verify, reducing the complexity of the algorithm and the rules to apply. If the reader looks up the “four-color theorem” in arXiv, he, or she, may be surprised with the amount of recent preprints on the topic.
Finally, the four-color theorem already has a prominent place in the history of mathematics. But the ultimate test will come with the passage of time, and there is still room for improvement. Maybe there is a smaller (optimal?) set of configurations. Maybe there is, after all, a proof that can be verified by hand. Maybe the current proofs can be explored visually and in a structured way so that even if computers are needed, no one can claim that a human can’t verify the computer calculations. Maybe the formalized proof will be more thoroughly reused and integrated into a broader graph theory formalization program. Maybe in a few years, proving the four-color theorem will be a standard assignment to undergraduate math students as part of their education, which will include some programming and formalization of maths. Time will tell.
* We have been unable to find any source code from the time of Appel and Haken. Robertson et al. claim that they would need to input many cases by hand to replicate Appel and Haken’s proof, and that, to their knowledge, no mathematician made a full revision of all of Appel and Haken’s work. Maybe some maths history archeologist will find the source code among Appel or Haken's personal effects. If any reader has any further information, we would be happy to amend this text.
** Coq will be renamed as Rocq Prover.
References
- [AH77a] Appel, Kenneth; Haken, Wolfgang (1977), Every Planar Map is Four Colorable. I. Discharging, Illinois Journal of Mathematics, 21 (3): 429–490, https://doi.org/10.1215/ijm/1256049011, MR 0543792
- [AHK77] Appel, Kenneth; Haken, Wolfgang; Koch, John (1977), Every Planar Map is Four Colorable. II. Reducibility, Illinois Journal of Mathematics, 21 (3): 491–567, https://doi.org/10.1215/ijm/1256049012, MR 0543793
- [AH77b] K. Appel, W. Haken. Microfiche supplement to Every planar map is four colorable. Part I and Part II. Illinois J. Math. 21(3): (September 1977). https://doi.org/10.1215/ijm/1256049023
- [AH77c] K. Appel, W. Haken. Microfiche supplement to Every planar map is four colorable. Illinois J. Math. 21(3): (September 1977). https://doi.org/10.1215/ijm/1256049024
- [AH77d] Appel, Kenneth; Haken, Wolfgang (October 1977), Solution of the Four Color Map Problem, Scientific American, vol. 237, no. 4, pp. 108–121, Bibcode:1977SciAm.237d.108A, https://doi.org/10.1038/scientificamerican1077-108
- [AH89] Appel, Kenneth; Haken, Wolfgang (1989), Every Planar Map is Four-Colorable, Contemporary Mathematics, vol. 98, With the collaboration of J. Koch., Providence, RI: American Mathematical Society, https://doi.org/10.1090/conm/098, ISBN 0-8218-5103-9, MR 1025335, S2CID 8735627
- [Doc21] Doczkal, Christian. A Variant of Wagner’s Theorem Based on Combinatorial Hypermaps. In 12th International Conference on Interactive Theorem Proving (ITP 2021). Leibniz International Proceedings in Informatics (LIPIcs), Volume 193, pp. 17:1-17:17, Schloss Dagstuhl – Leibniz-Zentrum für Informatik (2021) https://doi.org/10.4230/LIPIcs.ITP.2021.17
- [Gon05] Gonthier, Georges. A computer-checked proof of the Four Color Theorem. Inria. 2023 (first version 2005). HAL Id: hal-04034866, https://inria.hal.science/hal-04034866
- [Gon08] Gonthier, Georges (2008), Formal Proof—The Four-Color Theorem, Notices of the American Mathematical Society, 55 (11): 1382–1393, MR 2463991. https://www.ams.org/notices/200811/tx081101382p.pdf
- [Kem79] Kempe, A. B. On the Geographical Problem of the Four Colours. American Journal of Mathematics, Vol. 2, No. 3 (Sep., 1879), pp. 193-200 (9 pages) https://doi.org/10.2307/2369235
- [McM20] McMullen, Chris. The Four-Color Theorem and Basic Graph Theory. Zishka Publishing, 2020. ISBN 1941691099, 9781941691090
- [Ric23] Richeson. David S. The Colorful Problem That Has Long Frustrated Mathematicians. Quanta Magazine, March 29, 2023.
- [RSST95] Robertson, Neil; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin (1995, arXiv 2014), Discharging cartwheels. https://doi.org/10.48550/arXiv.1401.6485
- [RSST96] Robertson, Neil; Sanders, Daniel P.; Seymour, Paul; Thomas, Robin (1996), Efficiently four-coloring planar graphs, Proceedings of the 28th ACM Symposium on Theory of Computing (STOC 1996), pp. 571–575, https://doi.org/10.1145/237814.238005, MR 1427555, S2CID 14962541
- [Ste10] Steinberger, John. An unavoidable set of D-reducible configurations. Trans. Amer. Math. Soc. 362 (2010), 6633-6661. https://doi.org/10.48550/arXiv.0905.0043
- [Swa80] Swart, Edward R. The Philosophical Implications of the Four-Color Problem, The American Mathematical Monthly, 87:9, 697-707, (1980) https://doi.org/10.1080/00029890.1980.11995128
- [Tym79] Tymoczko, Thomas. The Four-Color Problem and Its Philosophical Significance. The Journal of Philosophy, Vol. 76, No. 2 (Feb., 1979), pp. 57-83. https://doi.org/10.2307/2025976
- [Wil14] Wilson, Robin. Four Colors Suffice: How the Map Problem Was Solved - Revised Color Edition, Princeton: Princeton University Press, 2014. https://doi.org/10.1515/9780691237565
- [Wil16] Wilson, Robin. Wolfgang Haken and the Four-Color Problem. Illinois Journal of Mathematics 60:1 2016, 149–178. https://doi.org/10.1215/ijm/1498032028. Available online also in Celebratio Mathematica https://celebratio.org/Appel_KI/article/796/

The video is available under the CC BY 4.0 license. You are free to share and adapt it, when mentioning the author (MaRDI).
In Conversation with Yves Bertot
Daniel Ramos speaks with Yves Bertot from the Inria Center at Université Côte d’Azur about formal proofs, what it means to maintain a proof repository, and how the FAIR data principles apply to formal proofs. In a fictional scenario, they also discuss whether AI could create formal proofs automatically.
Second NFDI Berlin-Brandenburg Network Meeting:
Ontologies and Knowledge Graphs
It was a surprise for us to learn that within Berlin and Brandenburg alone, more than 120 scientific and other institutions are involved in at least 25 out of the 27 NFDI consortia. Bringing everyone together to set up a regional network for collaboration on overarching topics was the main reason MaRDI initiated the first NFDI in Berlin-Brandenburg (NFDI_BB) meeting held on October 12th, 2023. It was at this meeting that “Ontologies and Knowledge Graphs” was quickly identified as a common topic of interest; especially since it has gained in importance due to the recent launch of the basic services (Base4NFDI) and the sub-project KGI4NFDI. Naturally, this was chosen as the subject of the second NFDI_BB workshop, held on July 11th, 2024, and hosted at the Weierstrass Institute for Applied Analysis and Stochastics (WIAS) in Berlin. A total of 35 participants, coming from 16 different consortia belonging to engineering sciences, humanities and social sciences, life sciences, and natural sciences, attended the meeting.
We started off with an interactive online survey, where the participants were asked several questions, one of them was building a word cloud of important terms related to ontologies and knowledge graphs. Wikidata, wikibase, sparql, and metadata were the ones mentioned most frequently. During the main part of the morning session, the topic “Ontologies and Knowledge Graphs” was presented in connection with the activities of the NFDI in four talks by Tabea Tietz, Lozana Rossenova, Olaf Simons, and Daniel Mietchen.
The afternoon session began with five short presentations on specific ontology concepts of the individual NFDI consortia (Sabine von Mering - NFDI4Biodiversity, Rolf Krahl - DAPHNE4NFDI, Sonja Schimmler - NFDI4DataScience, Frank von Hagel - NFDI4Objects and Aurela Shehu - MaRDI). After these presentations, the audience was polled on the use of (7 out of 24) and possible or planned development (9 out of 24) of ontologies as well as the role of artificial intelligence (AI). Interestingly, 12 out of 25 anticipate that in 10 years AI will use knowledge graphs and 5 out of 25 expect that it will even create them!!
It became clear, in the final discussion round, that this topic was very interesting to the participants and has the potential for cross-consortia collaboration. However, the development of domain-specific ontologies will evolve at different speeds, and this needs to be taken into account. The benefit of such subject-specific regional meetings resonated with everyone, and the interest to continue the series of NFDI_BB meetings in the future on the topic of Research Data Management in the curriculum was high.
If you want to be informed of the next meeting, subscribe to the NFDI_BB mailing list:
https://www.listserv.dfn.de/sympa/info/nfdi_bb.

Data❤️Quest at MEGA
MEGA is the acronym for Effective Methods in Algebraic Geometry. It is a series of biennial international conferences devoted to computational and application aspects of Algebraic Geometry. This year, it took place from July 29th to August 2nd at Max Planck Institute for Mathematics in the Sciences and the University of Leipzig.
During the five days of the conference, almost 200 participants attended plenary and parallel sessions on various topics. All abstracts and slides can be found online. Part of the program was a poster session at the University of Leipzig, Paulinum. MaRDI offered the game Data❤️Quest for all participants.


NFDI4Objects Berlin-Brandenburg
The first NFDI4Objects meets Friends network meeting will take place on November 7, 2024, in Berlin. This event offers ideas and networking on research data management (RDM) focused on archaeological and object-based data. It will showcase projects, discuss helpdesks, quality assurance, and RDM training.
More information:
- in German

NFDI Science Slam 2024 in Berlin
In cooperation with Berlin Science Week, NFDI4DS will host its annual Science Slam this October at the Weizenbaum Institute in Berlin. Researchers present their work in a simple, humorous way, inviting the audience to laugh, cry, and engage with NFDI and its consortia. This year’s motto is “Crossing Boundaries.”
More information:
- in English

GHGA Symposium 2024 in Heidelberg
The GHGA (German Human Genome-Phenome Archive) will hold a public symposium on 15 October 2024 in Heidelberg, focusing on topics related to enabling data sharing for health research in Germany and Europe. The event will feature presentations from GHGA members as well as renowned experts from various European biomedical data initiatives and projects, including the European Genomic Data Infrastructure (GDI), the German National Cohort (NAKO), NFDI4Health and the genome sequencing model project in Germany.
More information:
- in English


Robin Wilson's book Four Colors Suffice: How the Map Problem Was Solved offers an authoritative historical account of the four-color theorem history and the main mathematical ideas involved. The book is suitable for undergraduates. The 2014 edition includes colored images (the previous one only offered black and white images).
A more casual (and much shorter) read by the same author is his article Wolfgang Haken and the Four-Color Problem, published in 2016.
Quanta Magazine published the public outreach article The Colorful Problem That Has Long Frustrated Mathematicians by David S. Richeson in 2023. Quanta also produced a short video on the topic featuring the author.
The Numberphile YouTube channel published the video The Four Color Map Theorem, featuring James Grime, explaining the topic in layman's terms.
Chris McMullen's book "The Four-Color Theorem and Basic Graph Theory", published in 2020 by Zishka Publishing (ISBN 1941691099, 9781941691090), offers high-school-level puzzles and exercises related to the four-color theorem. It also includes an elementary proof of the theorem (which is not actually a proof, but it gives insights).
Mathigon (an online platform that combines an interactive textbook and a virtual personal tutor) offers an interactive course on graphs and networks, which includes a chapter on Map Coloring.

Welcome to the final Newsletter of the year and the first in a new series! Here in the MaRDI newsletter, we have been discussing ideas relevant to the MaRDI project: the FAIR principles, knowledge graphs, Research Data, and RDM in mathematics, from various perspectives. However, the MaRDI project has been running for over three years now, and it is already yielding some tangible services that can be tested and used.
So, with the turn of the season, we will introduce—starting now—with every newsletter issue a new research-data service for and from the mathematical community. To begin with, we have a look at a project born and raised at the University of Münster: the peer-reviewed knowledge graph of numerical algorithms MathAlgoDB. Based on the technology we discussed in our earlier specific issue on knowledge graphs, MathAlgoDB has been developed by MaRDI's scientific computing team. We have a look at their work, use cases, functionality, and future plans in our data date series, featuring articles as well as a video interview and demo of the service. So sit back, enjoy, and have a smooth transition into the new year! Happy holidays.
by Ariel Kahtan, licensed under CC BY-SA 4.0.
Since algorithms are the main topic of this newsletter issue, we are naturally interested to hear about your favorite algorithm in mathematics. Tell us in this one-click-survey:
What is your favorite algorithm?
In September, we asked you if you trust computer-based proofs in mathematics. Here are your results:


Three short stories on MathAlgoDB
With this newsletter issue, we start a new series of articles, each one focused on one particular MaRDI service. We will name the articles “N short stories on X”, where N ∈ ℕ and X ∈ {MaRDI services}. These will be fictional (or real) stories of people who discover, use, develop, or interact with some of the MaRDI services that we are featuring. We hope that these stories will relate to our readers, directly or indirectly, so they can also discover and use these services as they are intended: to make a mathematical researcher’s life easier, more pleasant, and better integrated within the community.
1. Surveying a subfield of mathematics
Brook is just starting a PhD in scientific computing, specifically in computerized tomography. Their advisor proposes they start getting a good grasp of the field and its classical algorithms. At the same time, the advisor is particularly interested in understanding some new results and comparing them to her own methods. Brook has received a list of references to articles from their advisor. However, following links from the available papers does not lead Brook to code in most cases. A couple of papers linked to personal repositories (which were not peer-reviewed or validated as the papers were), and there was not sufficient documentation to compare or to decide which one works best in each case.
Brook also browses around arXiv but finds it hard to judge whether all relevant material is there and how trustworthy the preprints are. There are no usable AMS or MSC identifiers, either. Which keywords should they use? And how good could the results possibly be?
Brook decides that their best approach is to follow academic social networks and attend conferences in the field. Experts will know which methods work best on what types of problems and can provide some insight into Brook’s advisor’s methods' standing against competitors.
Meeting experts at conferences is very useful, but maybe one of the best pieces of advice they get is to use a curated knowledge graph of numerical algorithms: MathAlgoDB. That would do exactly what Brook wishes to do: understand a field fully by linking papers to code, algorithms, implementations, and benchmarks. This is exactly what they have been looking for!
When Brook first opened the MathAlgoDB site, they had the preconceived idea that such a database should look like a table with columns (fields) like “name of the algorithm”, “inventor”, “book/paper of reference”, “software package that implements it”, etc., and one would have one row on that mental table per each algorithm. Brook also expected to find some search/filter function to prune the table and present the subset of algorithms matching their query.
Instead, Brook finds an interface where you can browse by Problem, Software package, or Algorithm… They start browsing around, and they click on Problems and “Linear Problem (Ax = b)” just to be on the familiar side of maths. They find a page where the subject “ Linear Problem (Ax = b)” is followed by a list of properties: “...specialized by: Symmetric Positive-Definite Linear Problem, Symmetric Linear Problem, etc” then “...is solved by: Biconjugate Gradients, Biconjugate Gradients Stabilized, etc.”
This is not just a database, but a knowledge graph, that is, the “entries” are not uniform registries that you can imagine as a table, but your mental image should be a graph, in which vertices represent different entities: algorithms, publications, software packages, mathematical problems, etc. The edges are named relations between the entities algorithm X solves problem Y, software Z implements algorithm Z, etc.
This knowledge graph model is more versatile than a database (even if, at a low level, the knowledge graph can be implemented on an SQL database). With the knowledge graph paradigm, we can traverse the graph by using meaningful pointers.
Brook now browses MathAlgoDB’s subfield of computerized tomography and finds that algorithms based on completely different ideas are available. Among these are Analytical methods based on filtered back-projection, Brute Force methods based on Algebraic Reconstruction Techniques, and exotic reconstruction methods like Fourier reconstruction or Cormack’s inversion formula. MathAlgoDB directs them to papers and books analyzing and comparing these methods.
For Brook, MathAlgoDB is a great tool for surveying an area of mathematics they are becoming familiar with. Once the knowledge graph becomes increasingly populated, it becomes possible to find all the relevant algorithms, references, and code in a particular field, and you can tailor your own survey study to your specific interests.
2. Let the world know about your algorithm
Christoph has recently started a tenure-track postdoc position. He has worked on his implementations of eigenvalue computation of sparse symmetric matrices for five years, so he has a good knowledge of the underlying theory, and he has developed highly proficient computational skills. Although he has quite a good grasp of his field, he also recognizes limitations when it comes to benchmarking. This is because implementing another researcher’s method in practice is not feasible for him due to time constraints, so it is difficult to precisely assess how his methods compare with those of other researchers. Also, appearances may be deceiving. For instance, implementing code from a verbose description in an article might result in a slower runtime than the author’s implementation, since computational tricks could have been applied by the author, but not mentioned in the paper. Christoph wonders whether it is possible to properly compare methods to find out which implementation of what algorithm is best – and if so, how. He hears whispers over coffee saying that on the upside of missing benchmarks, competitors will not be able to prove Christoph’s methods inferior either.
But Christoph does not consider this a good option. He firmly believes in good scientific practice and in honest comparisons that discern a more performant algorithm from a lesser one. He knows MathAlgoDB is at a valuable development stage, so he checks which algorithms and implementations are already there.
Christoph decides to take two actions. First, he documents his algorithms in MathAlgoDB. He finds that the editor interface of MathAlgoDB makes it easy for him to add to the knowledge graph pointers to his implementation code in GitLab, and to his publications using the DOI that his journal publisher provides. This makes his algorithms publicly available and well-documented. Within a few months of including his algorithms in MathAlgoDB, he starts noticing more inquiries by email from other researchers, and more citations to his work.
The second action requires a bit more time for him to finish. To make an unbiased evaluation of his algorithm, Christoph decides to develop a FAIR benchmark. His benchmark uses Open Data from the application problem that he seeks to solve, so anyone can review how the benchmark is set up, and reproduce the benchmark score independently. He applies the benchmark to his own algorithm, and also to all the competing algorithms that are listed in MathAlgoDB and include an implementation. As he suspected, his algorithm is the best one for the particular case of sparse symmetric matrices, and it is still quite robust in the non-sparse symmetric case. He publishes the results of this comparison, together with a documentation of the benchmark’s workflow in an arXiv article, and stores the program’s code and the open data he used on Zenodo. Finally, Christoph adds the benchmark problem to MathAlgoDB with pointers to the documentation, and connects it to all algorithms and software he compared, making everything findable and accessible.
By leveraging the infrastructure of MathAlgoDB and the FAIR benchmarks, he has obtained a new publication related to his algorithm, he has proven that his algorithm is better than competitors for his specific use case, and he has made it more findable and accessible, getting more citations as a bonus.
3. Get the right tool for your application
Agatha is an engineer with a solid mathematical background. She works in the manufacturing industry. For a particular project, she considers a control system for a mechanical component and wants to simulate it as a passive system.
She knows how to run numerical simulations of PDEs and use Finite Element Methods. Her simulations involve medium-sized input-output parameters, while the computation is done on a very fine discretization grid. With her current methods, and the computer cluster she can access, she can run one simulation every 7 days. Thus, she can only run a few simulations within the time frame of her project, but she would like to run dozens, maybe hundreds of simulations with different parameters. So she is looking for a way to reduce the dimensionality of the entire computation.
She starts researching what mathematical improvements she could apply and finds out about Model Order Reduction. From a quick look at general references, this does exactly what she needs. However, she is not an expert on the topic, and she does not know anyone close enough to ask for collaboration. Certainly, she will not want to implement new numerical methods for this task, so she needs some off-the-shelf solution that is also specifically tailored to her problem.
Then a colleague recommends looking at MathAlgoDB, and she decides to give it a try. Agatha originally thought that MathAlgoDB would be a kind of catalog for numerical algorithms. However, it is more than a curated list of algorithms. MathAlgoDB is a knowledge graph of algorithms, problems, publications, software repositories, and benchmarks.
Agatha starts by trying to find her exact problem of simulating mechanical components. Without surprise, she cannot find that exact problem in the database. She then tries to search for “model order reduction” and finds a list of graph entries classified by type: a few algorithms, lots of publications, and a list of Problems. She decides to browse the algorithms, looking for some keywords she can recognize.
She finds Passive Balanced Truncation, which seems familiar to her. The algorithm has an entry “is surveyed in:” and four publications: the inventing article and three publications that analyze it. The publications lead to a DOI identifier that sends you externally to the article or book in question. One of these looks like an interesting reading list, and Agatha spends a few minutes looking at that article.
That was useful, she thinks. She found that publication by searching semantically for a mathematical problem, and not by using a search engine and trying to match keywords in the article text, as she was used to.
Then she notices that the algorithm also had an “implemented by” entry, pointing to a software package. Agatha navigates there and then exits the knowledge graph again, this time to a GitHub repository with the code implementing the algorithm. It's still not what she is looking for, but again, the code documentation reveals some insights into the problem.
That is also neat, Agatha thinks. She is browsing references like a bibliography, but the references are not only “papers” but also code repositories, databases, etc. Also, these repositories are curated to follow FAIR principles, so they won’t likely disappear tomorrow. On top of that, most of this scientific research software is open source.
After a few hours of browsing MathAlgoDB, Agatha has found publication references, some repositories with code, and indirectly she has collected a list of names of experts in the field. She has enough material to read, program, and potential people to discuss for weeks of research.
One afternoon after work she goes for a drink with some colleagues. She tells them about her experience, still amazed that only some weeks before she was still relying on the popular web search engine to find repositories, names of experts, and everything that is not a publication. Indeed, she was also using it to find most of the publications she read. She was happy that someone put that infrastructure in place.
Her colleagues ask: “Well, did you find a solution within that knowledge graph of yours? Isn’t it better to just use a comprehensive, commercial software suit that implements most of the known and tested algorithms”. She replies, “Sometimes you buy a fancy expensive tool that does everything, you get used to it, and you use it for everything. Sometimes, you prefer to buy a very specialized tool that does one specific job, but much better than anything else. This knowledge graph is like asking a very knowledgeable shop assistant that knows all the tools in the market, and can recommend to you what you really need in your case. And in this case, tools and advice are for free!”.

(To improve the viewing experience, you may click on the settings symbol and choose the 1080p quality option.)
The video is available under the CC BY 4.0 license. You are free to share and adapt it, when mentioning the author (MaRDI).
In Conversation with Frank Wübbeling
Frank Wübbeling and Christiane Görgen have a look at the MaRDI service MathAlgoDB. What is it, how does it make your research life easier, who can contribute, and how? They have a chat on purpose and functionalities answering these questions, and look at a live demo.
MaRDI Annual Meeting 2024 in Kaiserslautern
In mid-November, MaRDI gathered at the Fraunhofer ITWM in Kaiserslautern for its 2024 annual meeting. The event, which took place from 18 to 20 November, welcomed members from all MaRDI Task Areas to reflect on achievements and define future priorities.
The first day featured internal sessions, including talks by Sven Hertling on knowledge graph construction and Daniel Mietchen on KGI4NFDI, as well as a guided tour of the Fraunhofer ITWM, including a driving simulator, and a networking dinner.
Tuesday's highlights included Allyson Lister's talk on the FAIRsharing Community Champions programme, John Voight's presentation on the LMFDB mathematical database, and Bernd Flemisch's insights into Jupyter4NFDI. The afternoon interactive marketplace showcased MaRDI's tools and services, such as the MaRDI Portal, MaRDI Station, and the MaRDI Knowledge Graph. It served to foster inner-MaRDI collaboration, for example tailoring the MaRDI Station to particular services, and to invite external researchers to try out first products.
The meeting concluded on Wednesday with Barcamp sessions and a Council meeting, providing space to refine strategies and solidify plans. The focus for the coming year is clear: further developing our services and promoting them to our community.
While Santa Claus was preparing to distribute gifts at the beginning of December, some twenty mathematicians met at TU Berlin to prepare the distribution of theorems. The highly interactive workshop "Lean meets MaRDI and OSCAR" saw these researchers discuss how to, in practice, onboard MaRDI's newest addition: Floris van Doorn's lean group at Uni Bonn. We have talked about some aspects of Lean and its library of formalized mathematics mathlib with Johan Commelin in our very first newsletter. Now, three years on, both Lean and the MaRDI Portal are ready to create first synergies.
First, the MaRDI Portal can function as a frontend to mathlib: have a look at the Cantor-Bernstein-Schroeder theorem, both an entry on wikidata and a formalized object in Lean. Rather than going via one of your favourite search engines to find the connection (say, google or leansearch.net), the Portal can render this result both in natural language and formalised mathematics, and it can additionally link it to authors and papers. This can be done systematically in the future for a large number of theorems, and workshop participants discussed technical details of that forthcoming implementation.
The other way around, Lean can of course also provide a rigorous basis, in particular proof, for the mathematics the Portal displays.
Second, the computer algebra system OSCAR can provide useful additional input to Lean by supplementing formal proofs with symbolic computations: one example of this is an existing interface created by Cedric Holle. It enables you from inside Lean to call OSCAR technology to calculate, say, the inverse of a matrix and, continuing in Lean, prove that the product of the original matrix with its inverse is equal to the identity in the respective underlying ring. Similar interoperability can be achieved with other object types like arrays, polynomials, and boolean operators.
The workshop participants, living on Santa Claus' chocolate and gummy bears, surveyed the directions these new synergies might span out in, sketched potential first projects, and learned about Lean, OSCAR, and the .mrdi file type on the way.
MaRDI at the Heidelberg Laureate Forum
The 11th Heidelberg Laureate Forum, held from September 22 to 27, 2024, brought together leading minds in mathematics and computer science for open, interdisciplinary exchanges. Throughout the week, young researchers engaged with renowned laureates, gaining valuable insights and expertise. The program featured a mix of lectures and panel discussions, complemented by interactive elements such as workshops and master classes, fostering collaboration and idea-sharing. The forum combined scientific dialogue, social interaction, and outreach activities, creating an atmosphere of inspiration and meaningful exchange.
Dr. Daniel Mietchen, a member of MaRDI, led a workshop titled “Open Science and Reproducibility”. In this interactive “bring your own data” session, early-career researchers in mathematics and computer science examined modern mathematical research through its data life cycle—from the initial conception of ideas to their publication and reuse. The workshop emphasized the importance of open science and collaboration, exploring the role of research data and best practices for organizing, documenting, and publishing it effectively. Participants analyzed their own mathematical work, assessed its reproducibility, and collaboratively derived strategies to enhance their research processes. The workshop slides are available on Zenodo.
Running parallel to the 11th HLF, the Heidelberg Laureate Forum Foundation presented an interactive exhibition, that takes visitors on an exciting journey through different topics in mathematics and computer science. MaRDI presented the “MaRDI Station”—a collaborative multiplayer game called "Citizen Quest: Together for a freer world". Players navigate a city environment, where citizens are confronted with dilemmas and issues related to mathematical research data and various other facets of freedom. The adventure begins aboard a mathematical ship docked in the city’s university quarter. Here, pioneers of academic freedom advocate for research data that are FAIR: findable, accessible, interoperable, and reusable. Players interact with various researchers and help them solve quests related to the FAIR data principles.
For more information or to rent the MaRDI Station for your institute or your event, contact us at newsletter@mardi4nfdi.de.
The 11th Heidelberg Laureate Forum offered an engaging platform for MaRDI to showcase its commitment to advancing open science, reproducibility, and FAIR data principles. It also underscored MaRDI’s role in fostering innovation and collaboration within the scientific community.


From Proof to Library Shelf
This catch-up workshop on Research Data Management for Mathematics will take place at MPI MiS in Leipzig from March 17-19, 2025. It will offer feature talks, hands-on sessions, and a Barcamp to discuss mathematical research data, present ideas and services, and network.
More information:
in German

Large Language Models and the future of scientific publishing
Various NFDI consortia are organizing the workshop "Large Language Models and the Future of Scientific Publishing". It will take place at DIPF Frankfurt on February 11, 2025. The workshop will bring together researchers and publishers to identify and address the upcoming challenges for journals and the increased demands on reviewers and the wider research community.
More information
- in English

FAIR Data Fellowships
Applications for this fellowship are open until January 10, 2025. These one-month fellowships, endowed with 1,500 Euros, offer researchers the opportunity to prepare their historical research data for publication with expert guidance on FAIR principles, structuring, and repositories from the five implementing institutions.
More information


The Research Data Management course Schlüsselqualifikation Forschungsdatenmanagement. Ein Kurs in 8 Teilen: Überblick was developed by Björn Schembera and held at the University of Stuttgart. The interdisciplinary course is aimed at students but can also be used and adapted for doctoral students, researchers, or other target groups and is openly licensed.
The article A group theory of group theory: Collaborative mathematics and the ‘uninvention’ of a 1000-page proof by Alma Steingart describes how finite group theorists resolved to produce a ‘second-generation proof’ to streamline and centralize the classification of mathematical objects known as finite simple groups.
In the podcast series Modellansatz (English: The modeling approach) by the research group of Scientific Computing at Karlsruhe Institute of Technology (KIT), you will experience firsthand what the researchers, graduates, and academic teachers at KIT puzzle about.